合分比技术
严格来说,合分比技术是一种代数处理方法,并不能算是三角体系中的一环,但是由于正弦定理及正弦定理系的存在,在化简的过程中三角比例式常常出现,这个时候如果合理运用合分比技术,再结合和差化积与积化和差,往往能使化简的表达式得以“跳出圈子,向前一步”,笔者喜欢称其为“破局”。(参考张景中先生《几何新方法和新体系》)
有题为证:
合分比技术的例子

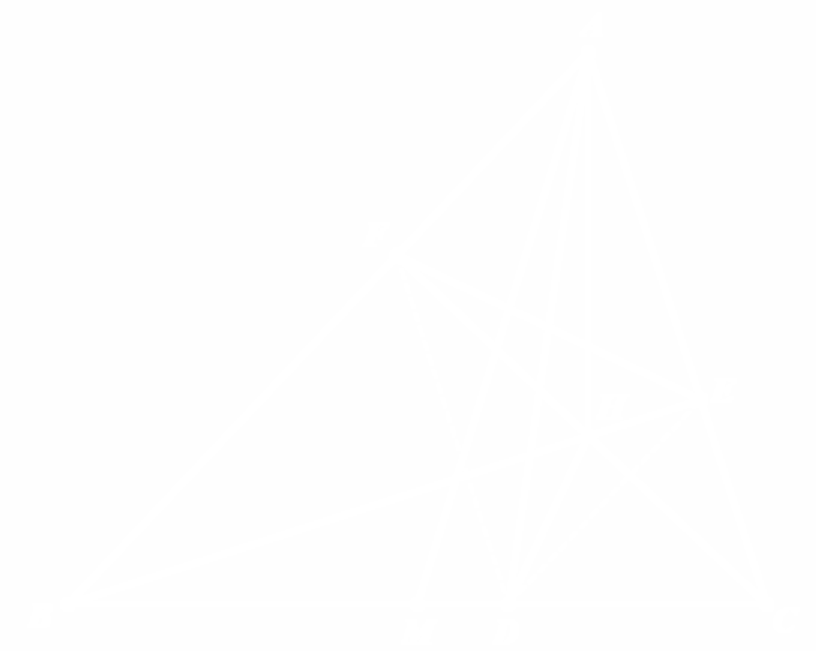
如图,在锐角\(\triangle ABC\) 中,\(AB>AC\),\(H\) 为垂心,\(AM\) 为中线,\(BE,CF\) 是高,\(D\) 在 \(BC\) 边上,满足 \(\angle CAD=\angle BAM\) 与 \(\angle ADH=\angle MAH\),求证:\(EF\) 平分线段 \(AD\)。
(2022-东南数学奥林匹克-P2)
问题之证明
由条件,\(AD\) 与 \(AM\) 为等角线,且 \(\triangle AEF\sim\triangle ABC\),故 \(AD\) 平分 \(EF\),从而即证明:\(AEDF\) 为平行四边形.
设 \(AD\cap EF=G\),由相似对应,\(\angle DGE=\angle AMC\),且 \(\angle ADH=\angle MAH\),两式相加得 \(\angle DGE+\angle ADH=90^{\circ}\),即 \(DH\perp EF\).
导角易得 \(\angle BHD=B,\angle CHD=C\),故由分角定理: $$ \dfrac{BD}{DC}=\dfrac{BH\sin B}{CH\sin C}=\dfrac{\sin B\cos B}{\sin C\cos C} $$ 而由陪位中线的知识知(事实上由分角定理也易得): $$ \dfrac{BD}{DC}=\dfrac{\sin^2 C}{\sin^2 B}=\dfrac{\sin B\cos B}{\sin C\cos C}(\^{*}) $$ 所证 \(\iff\dfrac{BD}{DC}=\dfrac{AE}{EC}\iff\dfrac{\sin^2 C}{\sin^2 B}=\dfrac{\sin C\cos A}{\sin A\cos C}\iff\dfrac{\sin^2 B}{\sin C\cos C}=\tan A.\)
对 \((\^{*})\) 式处理得: $$ \dfrac{\sin^2 C}{\sin B\cos B}=\dfrac{\sin^2 B}{\sin C\cos C}=\dfrac{\sin^2 C-\sin^2 B}{\sin B\cos B-\sin C\cos C} =\dfrac{\cos 2B-\cos 2C}{\sin 2B-\sin 2C}=\tan A, $$ 即 \(\dfrac{\sin^2 B}{\sin C\cos C}=\tan A\). 得证.